Post-hoc modification of linear models: combining machine learning with domain information to make solid inferences from noisy data

van Vliet M., Salmelin R.

DOI:10.1016/j.neuroimage.2019.116221

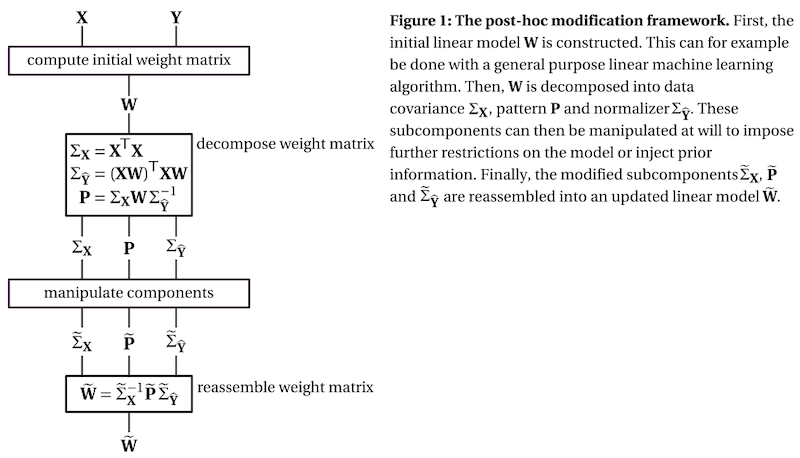
Abstract: Linear machine learning models are a powerful tool that can “learn” a data transformation by being exposed to examples of input with the desired output, forming the basis for a variety of powerful techniques for analyzing neuroimaging data. However, their ability to learn the desired transformation is limited by the quality and size of the example dataset, which in neuroimaging studies is often notoriously noisy and small. In these cases, it is desirable to fine-tune the learned linear model using domain information beyond the example dataset. To this end, we present a framework that decomposes the weight matrix of a fitted linear model into three subcomponents: the data covariance, the identified signal of interest, and a normalizer. Inspecting these subcomponents in isolation provides an intuitive way to inspect the inner workings of the model and assess its strengths and weaknesses. Furthermore, the three subcomponents may be altered, which provides a straightforward way to inject prior information and impose additional constraints. We refer to this process as “post-hoc modification” of a model and demonstrate how it can be used to achieve precise control over which aspects of the model are fitted to the data through machine learning and which are determined through domain knowledge. As an example use case, we decode the associative strength between words from EEG reading data. Our results show how the decoding accuracy of two example linear models (ridge regression and logistic regression) can be boosted by incorporating information about the spatio-temporal nature of the data, domain knowledge about the N400 evoked potential and data from other participants.

The full publication can be found in NeuroImage.